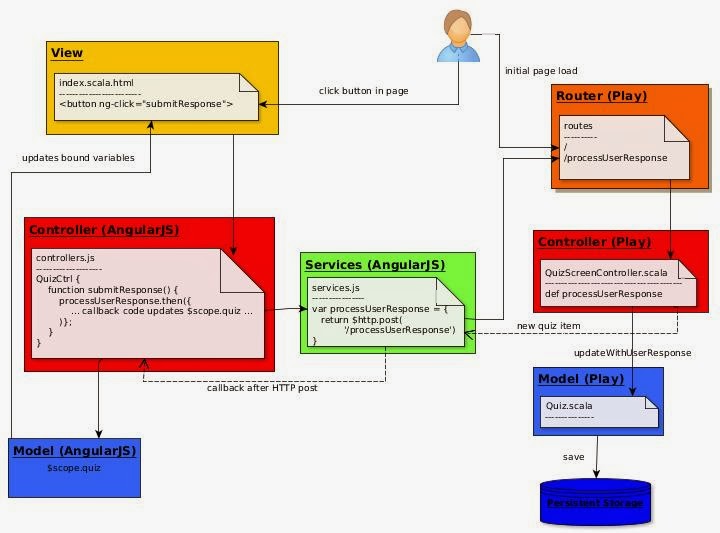
Fortunately things have got much easier in recent years with the emergence of helper software like Spark which will take your code and run it reliably in a cluster. This assumes that you follow certain conventions. Specifically, your program should be a pipeline of transformations between collections of elements, especially collections of key-value pairs. Such a collection in the Spark system is called an RDD (Resilient Distributed Dataset).
Spark is written in Scala. The API supports other languages too like Python and R, but let's stick with Scala, and illustrate how a sample problem can be solved by modelling the solution in this way and feeding the code to Spark. I will take a simplified task from the area of genomics.
DNA may be sequenced by fragmenting a chromosome into many small subsequences, then reassembling them by matching overlapping parts to get the right order and forming a single correct sequence.In the FASTA format, each sequence is composed of characters: one of T/C/G/A. Here are four sample sequence fragments:
>Frag_56
ATTAGACCTG
>Frag_57
CCTGCCGGAA
>Frag_58
AGACCTGCCG
>Frag_59
GCCGGAATAC
Can you see the overlapping parts? If you put the sequences together, the result is be
ATTAGACCTGCCGGAATAC.
A naive solution would do it the same way you do it in your head: pick one sequence, look through all the others for a match, combine the match with what you already have, look though all the remaining ones for a match again... and so on, until all sequences have been handled or there are no more matches.
Let's try a better algorithm, one which divides the solution into a number of tasks, each of which can be parallelized. First, you may want to download Spark. You will also need Scala and sbt.
We need Spark because the number of sequence fragments in a real-life scenario would be many millions. (However, I will continue to illustrate the algorithm using the toy data above.)
The skeleton of a Spark program looks like this:
import org.apache.spark.{SparkContext, SparkConf}
import org.apache.spark.rdd.RDD
object MergeFasta {
def main(args: Array[String]): Unit = {
val conf = new SparkConf().setAppName("MergeFasta")
val sc = new SparkContext(conf)
// The algorithm's code will go here.
}
}
main is the entry point. (The Scala extends App syntax also works, but the documentation recommends not using it.) The first thing any Spark program needs to do is get a reference to a SparkContext so it can send computations to the Spark execution environment.
Now, back to the algorithm. We start with a set of small sequences (see above). These would typically be read from a file and converted to an RDD. Throughout the program we try to keep all data wrapped in RDD data structures so Spark knows how to deal with and parallelize the processing. To get an RDD from a file, we can use Spark's own function,
sc.textFile("data.txt"), or use regular Scala code to read the file, parse it into a collection, and call sc.parallelize(anyScalaCollection).
By the way if you want to play about with Spark functions like this, the Spark software includes a REPL which you can fire up as follows:
$ spark-shell scala> val myRDD = sc.parallelize(List(1,2)) myRDD: org.apache.spark.rdd.RDD[Int] = ParallelCollectionRDD[1] at parallelize at <console>:27 scala> myRDD.collect() res2: Array[Int] = Array(1, 2)
Notice how the
collect() function is used to convert an RDD back into a Scala collection so we can view it.
Anyway, now that we have a starting RDD in the program, the first step of the algorithm is to compare each sequence with every other sequence to form a matrix. For each pair, calculate the number of characters at the end of the first sequence that match the characters at the beginning of the second (0 if there is no match). The matrix looks like this:
| Key sequence | Other sequences |
|---|---|
| ATTAGACCTG | (CCTGCCGGAA, 4), (AGACCTGCCG, 7), (GCCGGAATAC, 1) |
| CCTGCCGGAA | (ATTAGACCTG, 0), (AGACCTGCCG, 0), (GCCGGAATAC, 7) |
| AGACCTGCCG | (ATTAGACCTG, 0), (CCTGCCGGAA, 7), (GCCGGAATAC, 4) |
| GCCGGAATAC | (ATTAGACCTG, 0), (CCTGCCGGAA, 1), (AGACCTGCCG, 0) |
There are different ways you can build this matrix. Let's assume we have a function
matchingLength that calculates the number of characters that overlap between two sequences. Then we can use this code:
val seqList = seqSet.collect().toList
val matrix = seqSet.map(seq => (seq, seqList.filterNot(_ == seq)))
matrix.map {
case (keySeq, seqs) => (keySeq, seqs.map(seq => (seq, matchingLength(keySeq, seq))))
}
The nice thing is that if you are used to dealing with Scala collections, this will look very familiar. We are actually operating not on Scala collections but RDDs. More good news: RDDs are based on the FP technique of lazy evaluation, so no time is wasted on building intermediate collections. The work is postponed until you call
collect() or something similar.
The next step in the algorithm is this: for each row in the matrix, eliminate all values except the one with the longest match. Also eliminate inadequate matches, i.e. where the common part is not more than half the length of a sequence. The reduced matrix looks like:
| Key sequence | Sequence with overlap length |
|---|---|
| ATTAGACCTG | (AGACCTGCCG, 7) |
| CCTGCCGGAA | (GCCGGAATAC, 7) |
| AGACCTGCCG | (CCTGCCGGAA, 7) |
| GCCGGAATAC | (CCTGCCGGAA, 1) |
This transformation can be achieved using the
mapValues function:
val matrixMaximums = matrix.mapValues(seq => seq.maxBy(_._2))
The last line of the matrix is not a good match, so we can lop it off by applying a
filter:
matrixMaximums.filter { case (key, (seq, length)) => length > seq.length / 2 }
Now we have the sequences that we can put together to make the final sequence. We still need to get them in the right order though. Which is the first sequence? It will be any sequence that does not appear as a value anywhere.
val values: RDD[String] = matrix.values.map(_._1) val startingSeqs: RDD[String] = matrix.keys.subtract(values)
subtract is one of the many useful transformations available on an RDD, and does what you would expect. If you want to see all the available RDD transformations check the Spark API. There are examples of using each one here.We extract the starting sequence (signalling an error if there wasn't one and only one), and then "follow" that through the matrix: from
ATTAGACCTG to AGACCTGCCG to CTGCCGGAA to GCCGGAATAC where the trail ends. To implement this, we may call lookup on the RDD repeatedly inside of a recursive function that builds the String. Each sequence found is appended using the given length (7 in all cases here) to get a final sequence of ATTAGACCTGCCGGAATAC.
To see the final result we can just use
println . But how to run it? First compile it to a jar file. sbt is a good choice for building. The full code is available as an sbt project here. When you've cloned or downloaded that, call sbt package in the normal way and then issue the command:
spark-submit --class "MergeFasta" --master local[4] target/scala-2.11/mergefasta_2.11-0.1.jar
The
local[4] means that for test purposes we will just be running the program locally rather than on a real cluster, but trying to distribute the work to all 4 processors of the local machine.
When you run
spark-submit it will produce a lot of output about how it is parallelizing tasks. You might prefer to see this in the Web UI later. If you want to turn off excessive stdout logging in the meantime, go to Spark's conf directory, copy log4j.properties.template to log4j.properties and set log4j.rootCategory to WARN. Then you will just see the result at the end.
The next question is: how fast was it really? The Spark history server can look at the application logs stored on the filesystem and construct a UI. There is more about configuration here. But the main thing is to run this from the Spark root:
./sbin/start-history-server.sh
Then navigate in your browser to
http://localhost:18080/. You will see a list representing all the times you called spark-submit. Click on the latest run, the top one. Now there is a list of "jobs," the subtasks Spark parallelized and how long they took. The jobs run on RDDs will just be a few milliseconds each because of the strategy of deferring the bulk of the work to the end (lazy evaluation), where something like collect() is called.
When I first ran the code, by far the slowest thing in the list of jobs was the
count() on line 78, taking 2 seconds. count() is not a transformation: it is an action and it is not lazy but eager, forcing all the previously queued operations to be performed. So it is necessary to dig a bit deeper to find out where the true bottleneck is. Clicking on the link reveals a graph of what Spark has been doing:This suggests that the really slow thing is the
subtract operation on line 76. Let's look at that code again:val values: RDD[String] = matrix.values.map(_._1) val startingSeqs: RDD[String] = matrix.keys.subtract(values)
You can see that the
matrix RDD is used twice. The problem is that by default Spark is not keeping the matrix in memory, and it has to recompute it. To solve this, the cache function needs to be called just before the above code:matrix.cache()
After running everything again, the statistics breakdown looks like this:
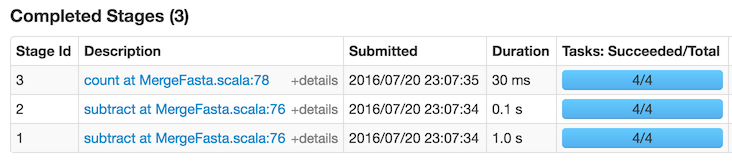
So, thanks to caching, the time has been nearly halved.
There are still many optimizations possible and perhaps you can think of a better algorithm entirely. However, hopefully this post has shown how Spark can be useful for parallelizing the solution to a simple problem. Again, the full code can be found here.